Solving Quadratic Equations Using the Square Root
Property
The Square Root Property can be used to solve a quadratic equation
written in the form x2 = a.
Property — Square Root Property
If x2 = a, then
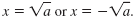
Here, a is a nonnegative real number.
Examples
If x2 = 7, then
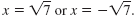
If (w + 6)2 = 3, then
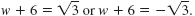
Here’s how to use the Square Root Property to solve a quadratic equation.
Procedure —
To Solve a Quadratic Equation Using the Square Root Property
Step 1 Write the equation in the form x2 = a.
Step 2 Use the Square Root Property.
Step 3 Write each answer in simplified form.
Step 4 Check each answer.
Example 1
Solve using the Square Root Property: x2 - 72 = 0
Solution
| Step 1 Write the equation in the form x2
= a.
Add 72 to both sides. |
x2 - 72 x2 |
= 0 = 0 |
| Step 2 Use the Square Root Property. |
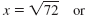 |
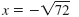 |
| Step 3 Write each answer in simplified form. Simplify each square root. |
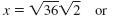
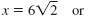 |
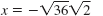
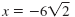 |
| Step 4 Check each answer. |
|
|
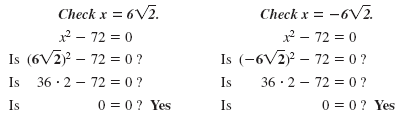
So, the equation x2 - 72 = 0 has two solutions,
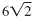 and
- and
-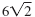 . .
Example 2
Solve using the Square Root Property: -4x2 + 64 = 0
Solution
| Step 1 Write the equation in the form x2
= a.
Subtract 64 from both sides.
Divide both sides by -4. |
-4x2 + 64
-4x2
x2 |
= 0 = -64
= 16 |
| Step 2 Use the Square Root Property.
|
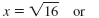 |
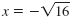 |
| Step 3 Write each answer in simplified form.
Step 4 Check each answer.
We leave the check to you. |
x = 4 or |
x = -4 |
So, the two solutions of -4x2 + 64 = 0 are 4 and -4.
Note:
Another way to write the solution is:
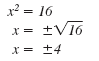
|
