Polynomials
Algebraic Expressions: The Building Blocks of Algebra
An algebraic expression is a collection of numerals, letters, grouping
symbols, and operators (such as +, -, ·, and
÷).
Here are some examples of algebraic expressions:
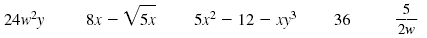
The algebraic expression 5x2 - 12 - xy3 has three terms:
5x2, -12, and -xy3
A term in an algebraic expression is a quantity joined to other quantities
by the operation of addition or subtraction.
The term -12 is called a constant term because it does not contain a
variable. Note that when a term is subtracted, a negative sign is attached to
the individual term.
The numeric factor of a term is called the coefficient of the variables of
that term.
For example, in the algebraic expression 5x2 - 12 - xy3, the coefficient of
x2 is 5 and the coefficient of xy3 is -1.
Note:
In the algebraic expression x2, the coefficient
of x2 is 1.
x2 = 1x2
Polynomials
A polynomial is a special kind of algebraic expression.
In a polynomial, each variable must have a whole number exponent.
Here are some examples of polynomials.
| 8x + 5 |
2x3 - wy2 + 7x - 6 |
24w2y |
-25 |
Note:
The polynomial 8x + 5
can be written 8x1 + 5x0.
An algebraic expression is not a polynomial if a variable is in the
denominator, inside absolute value bars, or under a radical sign.
For example, these algebraic expressions are not polynomials:
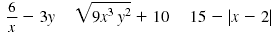
Polynomials with one, two, or three terms have special names.
| Name |
Number of terms |
Examples |
|
|
| monomial binomial
trinomial |
1 2
3 |
x,
x + 7,
x2 - 5x + 7, |
9wy2, 6x2 - 5,
-5x3y2 + 6xy - 9 |
13 4w2y
10wy3 |
The degree of a term of a polynomial is the sum of the exponents of the
variables in that term. For example,
• the degree of 8x2y4 is 6 because 2 + 4 = 6;
• the degree of 43y2 is 2. Note that 4 is not a variable so its
exponent, 3, does not affect the degree of the term.
Note:
In the expression 43y2, the exponent 3 does
not contribute to the degree of the term.
That's because 3 is the exponent of a
constant, not a variable.
The degree of a polynomial is equal to the degree of the term with the
highest degree.
For example, the degree of 8x2y4 - 5x3y + 43y2 is 6 because the term with
the highest degree has degree 6.
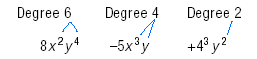
Note:
In 8x2y4 - 5x3y + 43y2, the term with the
highest degree is 8x2y4. It has degree 2 + 4 = 6.
Example
Find the degree of this polynomial: 13w4y3 + 5wy4
- y2 + 32
Solution
First, find the degree of each term.
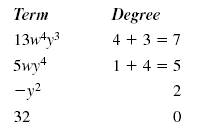
The term with the highest degree is 13w4y3. The degree of this term is 7.
Therefore, the degree of the polynomial is 7.
|
