Completing the Square
· Remember there
are three forms a parabola equation can have
y = ax 2 + bx + c
y = (x + h)(x + k)
y = a(x - h) 2 + k
· The first one is
the standard form. It provides us no details about the location of the
vertex. We can use the value of
a to determine the direction the parabola opens.
· The 2nd
is in factored form. The equation
could have been presented in 1st
form and was factored. If we set
this equation to zero (so that y = 0) we can use it find the roots (where the
parabola crosses the x axis)
· The 3rd
form is the vertex form of the
parabola. It tells us the direction of the parabola (the value of
a ) and the values of
h and k tells the location of the
vertex.
· The goal of
completing the square is to go from the 1st
form to the 3rd
form, or the vertex form.
o The process is
very mechanical
§ Arrange in
descending powers y = ax 2 + bx + c
§ Factor the
equation so the first term (the one with the power) has a coefficient of one
y = (ax 2 + bx) + c
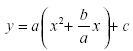
§ Now the process
really begins. Take half the middle term and add and subtract the square of that
number.
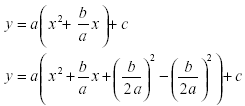
· By doing so you
have set up the equation for easier manipulation. You can see that we haven’t
changed the question, since we have added and subtracted the same number, we
have in effect added zero.
§ We will now
factor the first 3 terms, and move the 4th
outside the brackets
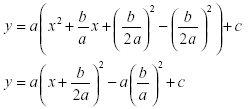
§ This is the final
product in a general form. It is to show you the
steps never change regardless of the coefficients!
word problems:
find the minimum product of 2 numbers whose difference is 8.
P = n(n-8)
= n 2 -
8n Ã
complete
the square to get P = (n-4)
2 -16.
the number will be 4 and the product will be 16.
|
