Solving Equations with Radicals and Exponents
The Even-Root Property
In solving the equation x2 = 4, you might be tempted to write x
= 2 as an equivalent
equation. But x = 2 is not equivalent to x2 = 4 because 22
= 4 and (-2)2 = 4.
So the solution set to x2 = 4 is {-2, 2}. The equation x2
= 4 is equivalent to the
compound sentence x = 2 or x = -2, which we can abbreviate as x
= ±2. The
equation x = ±2 is read “x equals positive or negative 2.â€
Equations involving other even powers are handled like the squares. Because
24 = 16 and (-2)4 =16, the equation x4 = 16 is equivalent to x
= ±2. So x4 = 16
has two real solutions. Note that x4 = -16 has no real solutions. The equation
x6 = 5 is equivalent to
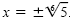 We can now state a general rule.
Even-Root Property
Suppose n is a positive even integer.
If k > 0, then xn = k is equivalent to
 .
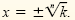If k = 0, then xn = k is equivalent to x = 0.
If k
< 0, then xn = k has no real solution.
Helpful hint
We do not say, “take the
square root of each side.â€We
are not doing the same thing
to each side of x2 = 9 when
we write x = ±3. Because there is only one odd
root of every real number, you
can actually take an odd root
of each side.
Example 1
Using the even-root property
Solve each equation.
a) x2 = 10
b) w8 = 0
c) x4 = -4
Solution
| a) x2 |
= 10 |
|
| x |
 |
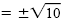Even-root property |
The solution set is {- ,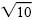
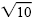 }, or
{±}.
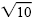| b) w8 |
= 0 |
|
| w |
= 0 |
Even-root property |
The solution set is {0}.
c) By the even-root property, x4 = -4 has no real solution. (The fourth power of
any real number is nonnegative.)
|
