In the quadratic formula, the radicand, b2 - 4ac, is called the discriminant
of the quadratic equation ax2 + bx + c = 0.
We can use the discriminant to determine the nature of the solutions of a
quadratic equation without having to solve the equation.
Discriminant
Solutions
b2 - 4ac > 0
two different real numbers
b2 - 4ac = 0
two identical real numbers
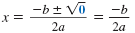b2 - 4ac < 0
no real number solutions
If the discriminant is a perfect square, the
solutions will not only be real numbers,
they will also be rational numbers.
Example
Use the discriminant to determine the nature of the solutions of this
quadratic equation: -2x2 - x + 7 = 0
Solution
The equation has the form ax2 + bx + c = 0 where a
= -2, b = -1, and c = 7.
Substitute the values of a, b, and c into the discriminant and simplify.
b2 - 4ac
= (-1)2 - 4(-2)(7)
= 1 + 56
= 57
The discriminant is 57, a positive number.
So the equation -2x2 - x + 7 = 0 has two unequal real number solutions.
Start solving your
Algebra Homework in next 5 minutes!
Buy
Algebrator now:
Instant download and optional CD
Only $39.99
Click to Buy Now:
Goods and services provided by Softmath (TX, USA).
Sold by 2CheckOut.com Inc. (Ohio, USA).
Attention: We are
currently running a special promotional offer
for algebrahomework.org Visitors -- if you order
Algebrator by midnight of
July 3rd
you will pay only $39.99
instead of our regular price of $58.99 -- this is $19 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minutes of live math tutoring from tutor.com!
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebrator is:
Step 1
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
Step 2 :
Let Algebrator solve it:
Step 3 : Ask for an explanation for the steps you don't understand:
Algebrator can solve problems in all the following areas:
simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
factoring and expanding expressions
finding LCM and GCF
operations with complex numbers
(simplifying, rationalizing complex denominators...)
solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
solving a system of two and three linear equations
(including Cramer's rule)
