Finding the GCF of a Set of Monomials
Finding the GCF of a Set of Numbers
Recall that the greatest common factor (GCF) of a set of numbers is the
greatest number that is a factor of all the numbers in the set.
Procedure —
To Find the Greatest Common Factor (GCF) of a Set of Numbers
| Step 1 |
Write the prime factorization of each number.
|
| Step 2 |
List each common prime factor the LEAST number of times
it appears in any factorization.
|
| Step 3 |
Multiply the prime factors in the list.
If two numbers have no common prime factor, then their GCF is 1. |
Example
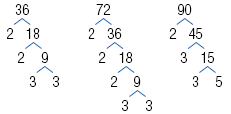
Find the GCF of -36, 72, and -90.
Solution
|
Step 1 Write the prime factorization of each
number.
Prime factorization applies to natural
numbers, so first write each negative
number as -1 times its opposite.
|
-36
-90 |
= -1 · 36 = -1
· 90 |
| A factor tree may be helpful in finding the prime factorizations. |
|
 |
-36
72
-90 |
= -1 = 2
= -1 |
· 2 · 2 · 3 · 3
· 2 · 2 · 3 · 3
· 2 · 3 · 3 · 5 |
| Step 2 List each common prime factor the LEAST number of times it
appears in any factorization. |
| |
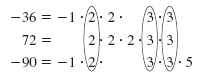 |
| The common prime factors are 2 and 3. The least number of times that 2 appears in a factorization is once.
So, 2 appears once in the list.
The least number of times that 3 appears in a factorization is twice.
So, 3 appears twice in the list.
Here is the list: 2, 3, 3 |
|
| Step 3 Multiply the prime factors in the list.
Thus, the GCF of -36, 72, and -90 is 18.
To see that 18 is a common factor of -36, 72, and -90, we write each as a
product using 18 as one of the factors. |
2 · 3 · 3
-36
72 |
= 18
= 18 · (-2)
= 18 · 4 |
We can use a similar procedure to find the GCF of a set of monomials that
contain variables.
Procedure —
To Find the Greatest Common Factor (GCF) of a Set of Monomials
Step 1 Write the factorization of each monomial.
Step 2 List each common factor the LEAST number of times it
appears in any factorization.
Step 3 Multiply the factors in the list.
If two monomials have no common factors, other than 1, then their
GCF is 1.
|
